Definitions

A thin lens is an idealized optical lens whose thickness is negligible compared to its focal length and radii of curvature. This simplification allows refractions to be treated as occurring at a single plane, called the principal plane. I also means that we can neglect the diffraction in the lens. Thin lenses obey the lens maker’s equation and the Gaussian lens formula: $$ {{\frac{1}{f} = \left( n - 1 \right) \left( \frac{1}{R_1} - \frac{1}{R_2} \right) }}$$ $$ \frac{1}{f} = \frac{1}{d_o} + \frac{1}{d_i} $$ where:

• \(f\) is the focal length,
• \(n\) is the refractive index of the lens,
• \(R_1\) and \(R_2\) are the radii of curvature of the lens surfaces,
• \(d_o\) and \(d_i\) are the object and image distances.

If we look at the scheme below, we find the expression of the output profil \(A_L'(x,y)\) as function of the input profil \(A_L(x,y)\).

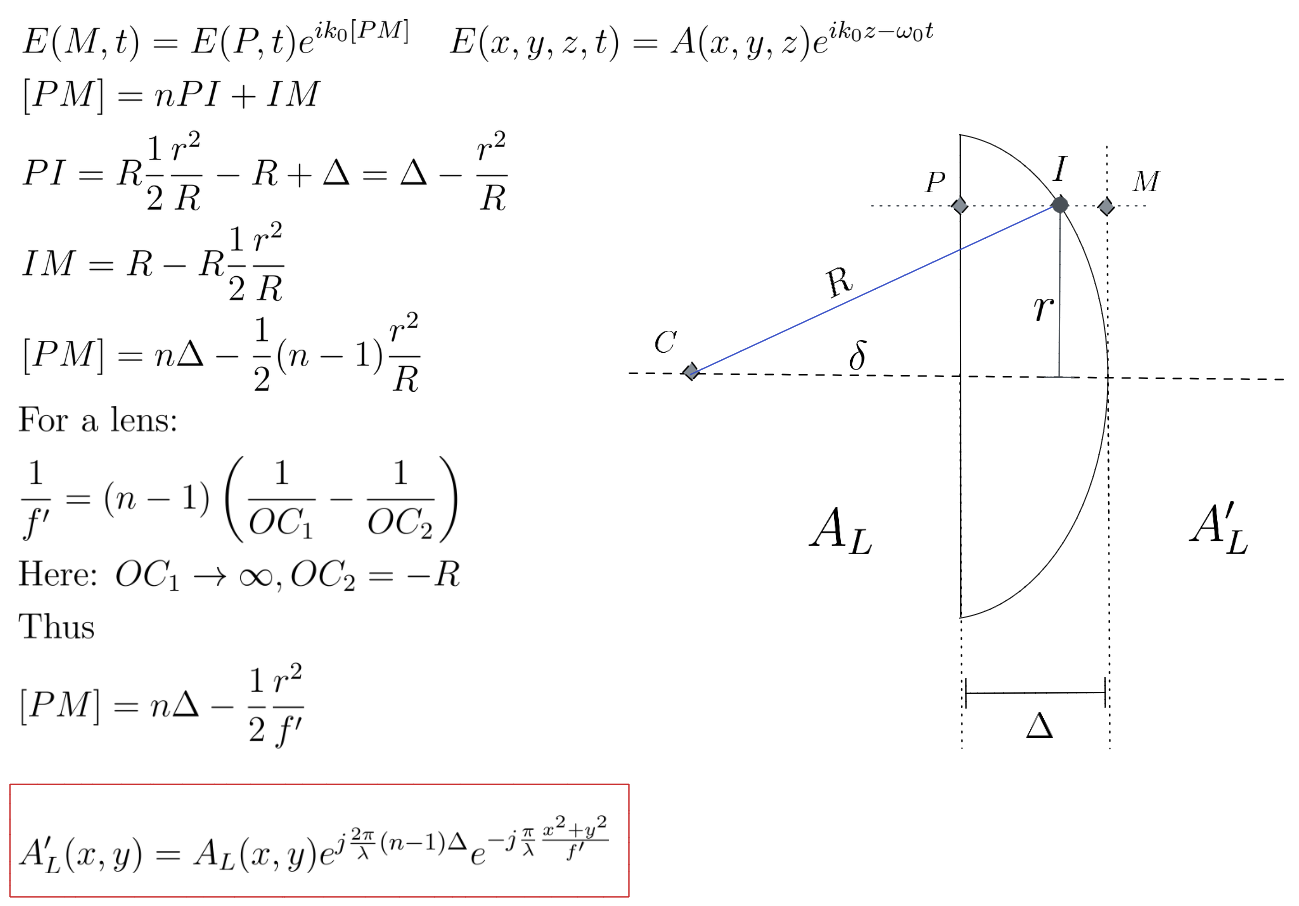
The lens effect is then given by :$$A'_L(x,y)={{A_L(x,y)e^{j\frac{2\pi}{\lambda}(n-1)\Delta}\underbrace{e^{-j\frac{\pi}{\lambda}\frac{x^2+y^2}{f'} } }_{\text{quadratic phase} } }}$$
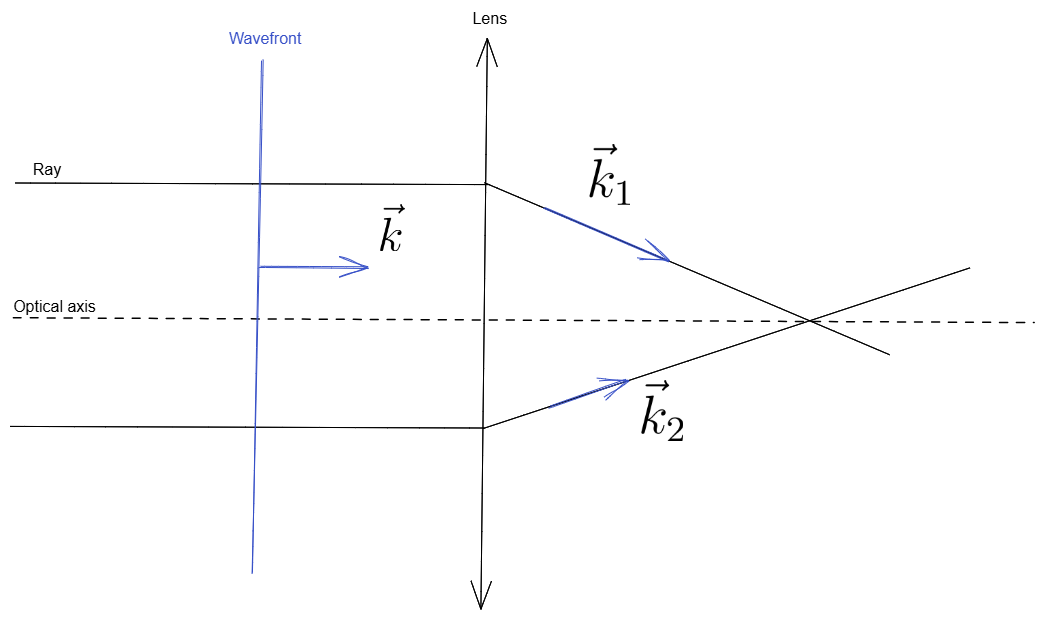
This lens effect is, in fact, a nonlinear effect because it generates new frequencies, as illustrated in the figure below.

Focal point

What do we observe in the focal plane ?

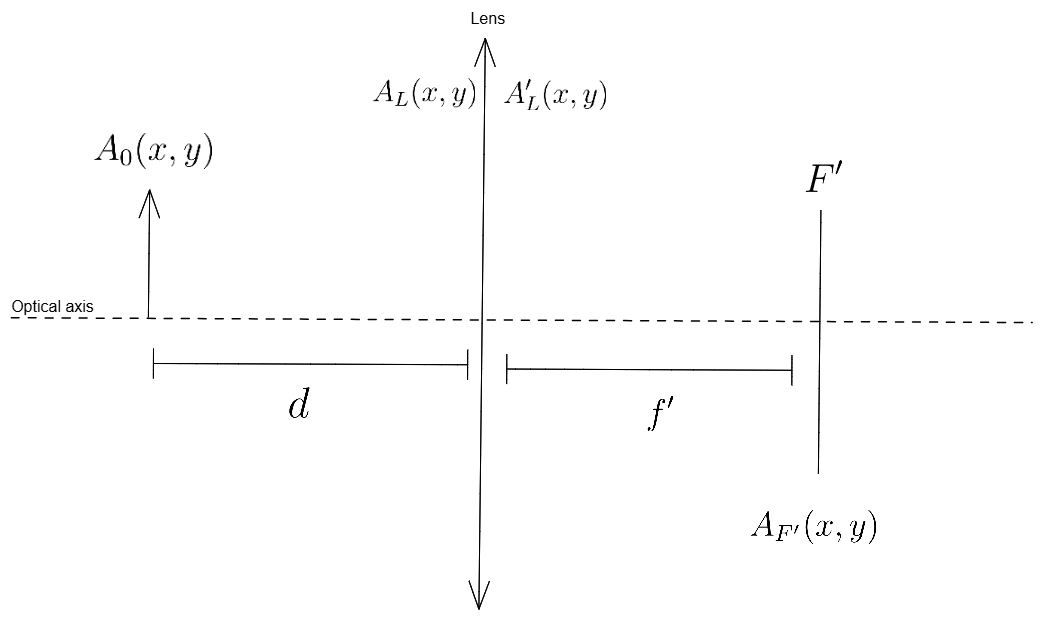
There are three steps: The object \(A_0\)​ is diffracted over a distance \(d\) to become \(A_L\), then it passes through the lens to become \(A'_L\), and finally, it is diffracted until it reaches the focal plane \(A_F'\).
By starting from the end, in the focal plane \(F'\), \(A_F'\) is the diffracted envelop of \(A_L'\) such that:
$$A_F'=\frac{1}{_\lambda f'}\iint_{-\infty}^{\infty}A_L'(x',y')e^{i\frac{\pi}{\lambda f'}\left[(x-x')^2+(y-y')^2\right]}dx'dy'\quad\text{Fresnel diffraction}$$
And \(A_L'\) is given by the lens effect on \(A_L\):
$$A_F'=\frac{1}{_\lambda f'}\iint_{-\infty}^{\infty}A_L(x',y')e^{\overbrace{-j\frac{\pi}{\lambda f'} (x'^2+y'^2)}^{\text{lens effect} } } e^{j\frac{\pi}{\lambda f'}\left[(x-x')^2+(y-y')^2\right]}dx'dy'$$
Which give:
$$A_F'=\frac{1}{_\lambda f'}e^{j\frac{\pi}{\lambda f'}(x^2+y^2) }\underbrace{\iint_{-\infty}^{\infty}A_L(x',y')e^{-j\frac{2\pi}{\lambda f'}(xx'+yy') }dx'dy'}_{FT(A_L)\left[f_x=\frac{x}{\lambda f'},f_y\frac{y}{\lambda f'}\right]}$$
Finally, we have:
$$|A_F'|^2=\frac{1}{(\lambda f')^2}|FT(A_L)|^2\quad \text{ Fraunhofer }$$
That's why we talk about Fourier Optics ! At the focal plane, a lens effect is equivalent to a Fourier transform.
We can also easly show that the link between \(A_0\) and \(A_F'\) is :
$$A_F'={{\frac1{j\lambda f'}e^{j\frac{\pi}{\lambda f'} }\left(1-\frac{d}{f'}\right)(x^2+y^2)\tilde A_0}}$$
Where \(\tilde A_0\) is the Fourier transform of \(A_0\). We see here that the phase profil stay unchanged only at the focal object plane.

Paradox

You should notice that there is a paradox when we think about the previous result. Our result means that we have the Fourier transform of the object in the focal plane. However, in the real life, we only observe the image of the initial object.
So what are the keys to solve this paradox ?

Operture of lenses

Gaussian beam

Applications

Shack-Hartmann